Desetinná čísla
- Které dvě části má desetinné číslo?
- Každé desetinné číslo je složeno z celé části. Necelé části desetinných čísel, se kterými jste dosud počítali, byly tvořeny desetinami a setinami. Například číslo 16,32 je složeno takto:
- 16,32 = 16 + 0,32
- Číslo 16 je celá čát a číslo 0,32 necelá část původního čísla. Necelá část je složena ze 3 desetin a 2 setin.
- Co jsou tisíciny, desetitisíciny, statisíciny,...?
- Například: Protože 1m = 10dm, platí 1dm = 0,1m.
- Protože 1m = 100cm, platí 1cm = 0,01m.
- Rozdělíme-li celek na 1000 stejných částí, bude každá část tisícinou původního celku. Jednu tisícinu apíšeme desetinným číslem
- 0,001 (čti ,,žádná celá, jedna tisícina"
- nebo ,,nula celá, jedna tisícina").
- Platí tedy:
- 1 : 1 000 = 0,001
- Například:
- Protože 1m = 1 000mm, platí 1mm = 0,001m.
- Protože 1kg = 1 000g, platí 1g = 0,001kg.
- V rozdělování celku na menší, stejně velké díly můžeme pokračovat i dále. Při rozdělení na 10 000 stejných dílů dostaneme desetitisíciny, na 100 000 stejných dílů Istotisíciny, na 1 000 000 stejných dílů miliontiny (původního celku). V matematice to zapíšeme rovnostmi:
- 1 : 10 000 = 0,0001 (čti ,,žádná celá, jedna desetitisícina")
- 1 : 100 000 = 0,000 01 (čti ,,žádná celá, jedna stotisícina")
- 1 : 1 000 000 = 0,000 001 (čti ,,žádná celá, jedna miliontina")
- V praxi se díly menší než miliontiny nezapisují jako desetinná čísla, ale vyjadřují se pomocí mocnin. Naučíte se to v sekundě.
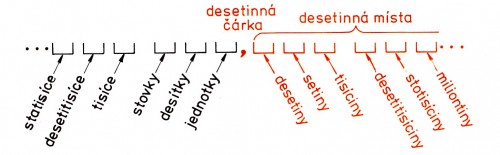
- Zápis ,,dlouhého" desetinného čísla bude přehlednější, když každou trojici číslic za desetinnou čárkou oddělíme malou mezerou. Dobře víte, že podobně se seskupují i číslice před desetinnou čárkou.
- Desetiny, setiny, tisíciny, desetitisíciny,... jsou jednotky řádů na místech za desetinnou čárkou. Těmto místům říkáme desetinná. (Jednotky na místech řádů před desetinnou čárkou už znáte: jsou to jednotky, desítky, stovky, tisíce, ...)
-
-
V následující tabulce jsou znovu zapsána desetinná čísla, která vyjadřují jednotky řádů za desetinnou čárkou:
-

- Jaké jsou vztahy mezi desetinami, setinami, tisícinami,...?
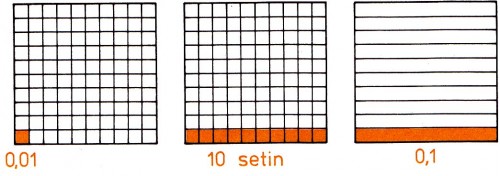
- Nejprve vysvětlíme, z kolika setin je složena 1 desetina. Na obrázku vidíte čtverec rozdělený na 100 stejných čtverečků. Jsou to setiny celého čtverce.
-
-
0,1 = 0,10
- Všimněte si rovnosti napravo. K zápisu čísla 0,1 jsme zprava připsali jednu nulu. Tím jsme ,,přidali" 0 setin, takže jsme původní číslo nezměnili. Zápis 0,10 nám napovídá, že jde o číslo složené z 10 setin. (Přečteme číslo za desetinnou čárkou a pojmenujeme ho podle posledního ,,obsazeného" místa.)
- Připisováním dalších nul objevíme tyto vztahy:
- 0,1 = 0,100 1 desetina je 100 tisícin
- 0,1 = 0,100 0 1 desetina je 1 000 desetitisícin
- 0,1 = 0,100 00 1 desetina je 10 000 stotisícin
- 0,1 = 0,100 000 1 desetina je 100 000 miliontin
- Stejně snadno například zjistíme, z kolika stotisícin je složena 1 setina:
- 0,01 = 0,010 00
- K číslu 0,01 jsme připisovali nuly tak dlouho, až jsme se ,,dostali" ke stotisícinám. Vidíme, že 1 setina je 1 000 stotisícin.
- Jak zapisujeme a čteme desetinná čísla?
- Zápis 0,007 vyjadřuje číslo, složené ze 7 tisícin. Přečteme ho ,,žádná celá, sedm tisícin". Podobně čteme další čísla:
- 0,000 3 ,,žádná celá, tři desetitisíciny"
- 0,000 04 ,,žádná celá, čtyři stotisíciny"
- 5,000 009 ,,pět celých, devět miliontin"
- Poslední číslo je složeno z pěti jednotek a devíti miliontin.
- Složitější situace nastane, když je za desetinnou čárkou více nenulových číslic.
- Víte již, že číslo 0,35 (složené z tří desetin a pěti setin) nečteme ,,žádná celá, tři desetiny, pět setin",ale jednodušeji: ,,žádná celá, třicet pět setin". Podobně číslo 0,035 složené ze tří setin a pěti tisícin přečteme ,,žádná celá, třicet pět tisícin".
- Podívejte se, jak čteme další desetinná čísla:
- 1,328 ,,jedna celá, tři sta dvacet osm tisícin"
- 4,000 204 ,,čtyři celé, dvě stě čtyři miliontiny"
- 7,408 25 ,,sedm celých, čtyřicet tisíc osm set dvacet pět stotisícin"
-
- Vysvětlíme, na čem je čtení necelých částí založeno. Například číslo 0,328 je složeno ze tří desetin, dvou setin a osmi tisícin. Protože 3 desetiny jsou 300 tisícin a 2 setiny jsou 20 tisícin, je celkový počet tisícin roven 300+20+8, tj. 328.
- Obvyklým zápisům desetinných čísel někdy říkáme zkrácené. Napřklad 24,561 je zkrácený zápis čísla, které je složeno ze dvou desítek, čtyř jednotek, pěti desetin, šesti setin a jedné tisíciny. ,,Podrobněji" je můžeme zapsat jako součet:
- 24,561 = 2 . 10 + 4 . 1 + 5 . 0,1 + 6 . 0,01 + 1 . 0,001
- Napravo stojí rozvinutý zápis daného čísla.
- Prohlédněte si rozvinuté zápisy dalších dvou čísel:
- 98,745 6 = 9 . 10 + 8 . 1 + 7 . 0,01 + 5 . 0,001 + 6 . 0,000 1
- 102,201 = 1 . 100 + 2 . 1 + 2 . 0,1 + 1 . 0,001
- Všimněte si, že v posledním zápisu jsme vynechali sčítance 0 . 10 a 0 . 0,01.
- (V rozvinutém zápisu čísla nejsou desítky a setiny zastoupeny.)
- Jak porovnáváme desetinná čísla?
- Již ze základní školy víte, že ze dvou různých čísel je vždy jedno menší a druhé větší. Zapisujeme to nerovnostmi. Například číslo 0,57 je větší než číslo 0,28, noboli číslo 0,28 je menší než číslo 0,57:
- 0,57 > 0,28 neboli 0,28 < 0,57
- Jak poznáme, které ze dvou čísel je menší a které větší?
- Nerovnost 1,28 > 0,95 je jasná, neboť první číslo má větší celou část než druhé.
- Čísla 3,45 a 3,15 však mají celou část stejnou, proto se podíváme, které z nich má více desetin. Je to číslo 3,45, takže 3,45 > 3,15.
- Čísla 2,183 a 2,182 9 se shodují v celých částech, desetinách i setinách. Proto je porovnáme podle počtu tisícin: 2,183 > 2,182 9.
- Jak zaokrouhlujeme desetinná čísla?
- Víte již, že přesné číselné údaje v praxi často nahrazujeme jejich přibližnými hodnotami. Při tom je nutné čísla správně zaokrouhlovat.
- Naučili jste se již zaokrouhlovat přirozená čísla. Připomeňme, jak například zaokrouhlujeme číslo 8 734 na desítky, stovky a tisíce:
- 8 734 = 8 730 (zaokrouhleno na desítky)
- 8 734 = 8 700 (zaokrouhleno na stovky)
- 8 734 = 9 000 (zaokrouhleno na tisíce)
- Desetinná čísla zaokrouhlujeme podle stejných pravidel. Vysvětlíme je při zaokrouhlování čísla 42,817 5:
- Při zaokrouhlení na jednotky je rozhodující číslice 8 na místě desetin. Proto zaokrouhlíme nahoru:
- 42,817 5 = 43
- Při zaokrouhlení na desetiny je rozhodující číslice 1 na místě setin. Proto zaokrouhlíme dolů:
- 42,817 5 = 42,8
- Při zaokrouhlení na setiny je rozhodující číslice 7 na místě tisícin. Proto zaokrouhlíme nahoru:
- 42,817 5 = 42,82
- Při zaokrouhlení na tisíciny je rozhodující číslice 5 na místě desetitisícin. Proto zaokrouhlíme nahoru:
- 42,817 5 = 42,818
- Někdy říkáme, že jsme desetinné číslo zaokrouhlili na určitý počet desetinných míst. Na jedno desetinné místo znamená na desetiny, na dvě desetinná místa na seiny atd.

Komentáře
Přehled komentářů
je to nepochopitelné
vbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
(logan, 5. 11. 2014 7:32)qwertzuiopasdfr
Miliontiny
(HonzaS9, 17. 9. 2014 18:37)A jak se značí víc čísel na milion třeba 3,a nějaké miliony prostě ve věčim čísle
Ahoj.
(Ordil, 13. 11. 2013 17:27)Ahoj jsem velitelka několika firem a ty byses sice nehodila ani do jedné ale mohla bys nějak pomoct.Pokud bys souhlasila napiš mi prosím na můj email tedy na náš email - Popularit@email.cz tvé schopnosti by mohly pomoct
ahoj
(Brepta21, 12. 10. 2013 13:58)
Prosím reknete z jake knihy to berete ja to potrebuju taky!!!!!!!!!!!!!
dekuji brepta21
dekuju
(tomas, 19. 12. 2012 20:47)dekuji opravilsem si 5 na 1 moc mito pomohlo dekuju mnohokrat
pomoc
(lucie, 15. 4. 2012 11:27)ahojte toto jaksi nechapu pomozte mi volejte mi na cislo 739 150 702 dekuji a nak mi to vysvetlete dekuju lucie
čísla osa se zápornýma čísly
(pepa, 18. 3. 2012 19:29)ahoj , mam dotaz na autora tohoto članku(tohoto webu) kde ste sehnali tyto informace z jake knihy, potřeboval bych nějaku taku knihu kde by bylo vše dopodrobna vysvětleno jako tady dam vam zde mul MAIL když to tak mi pišněte na nho a poradtě z jake knihy čerpate učivo a teoriii zakladní školy díky moc. MEIL: pepa-miropsov@seznam.cz
desetina čísla-
(lukáš, 6. 3. 2012 18:24)ahojte lidičky, mam dotaz na autora tohoto članku(tohoto webu) kde ste sehnali tyto informace z jake knihy, potřeboval bych nějaku taku knihu kde by bylo vše dopodrobna vysvětleno jako tady dam vam zde mul MAIL když to tak mi pišněte na nho a poradtě z jake knihy čerpate učivo a teoriii zakladní školy díky moc. MEIL: carl.baker@seznam.cz
Děkuji
(Marcelka, 18. 1. 2012 17:28)Moc vam dekuji pomohlo mi to opravit si 4 na 2 ddiiiiiiiiiiiikkkkkkkkkkyyyyyyyyyyy
Děkuji
(terka, 14. 12. 2011 7:31)Děkuji, díky tady uveřejněným údajům jsem si opravila 4 z pololetní práce v matematice.

čago
(jasmina hanesova, 5. 3. 2015 18:27)